Limite descreve o comportamento de uma função matemática à medida que se aproxima de um ponto específico. Pode ser definido como o valor que a função se aproxima à medida que os valores de entrada se aproximam cada vez mais de um determinado valor. Este conceito é crucial para o cálculo e é a base para muitas outras teorias matemáticas.
O limite é essencial para compreender a continuidade, a diferenciabilidade, a integração e vários aspectos da análise matemática.
Neste blog, analisaremos os principais conceitos de limites e exploraremos várias técnicas para avaliá-los. Forneceremos muitos exemplos para uma melhor compreensão deste conceito.
Definição de Limite com sua Notação Matemática
Seja f uma função definida em algum subconjunto dos números reais, exceto possivelmente em um ponto c dentro desse subconjunto. O limite de f(x) quando x se aproxima de c é L, se para cada ε > 0, existe um δ > 0 tal que se 0 < |x – c| < δ, então |f(x) – L| < ε.
Em termos simples, um limite refere-se ao valor que uma função ou sequência se aproxima à medida que sua entrada ou índice se aproxima de um determinado valor.
A noção de limite é:
limão x → cf(x) = eu
( leia como “limite de f(x), quando x se aproxima de c é L”).
Tipos de limite
Existem vários tipos de limites usados para descrever vários conceitos e propriedades. Aqui estão alguns dos tipos comuns de limites:
- Limites Unilaterais
Os limites unilaterais descrevem o comportamento de uma função à medida que ela se aproxima de um ponto em apenas uma direção. Está dividido em dois tipos.
Limite à esquerda
Um limite à esquerda é o limite de uma função à medida que ela se aproxima de um ponto pela esquerda. Está escrito como :
limão x → c – f(x)
Limite à direita
Um limite à direita é o limite de uma função à medida que ela se aproxima de um ponto pela direita.
limão x → c + f (x)
- Limites bilaterais
Esses limites descrevem o comportamento de uma função à medida que a variável independente se aproxima de um ponto específico tanto do lado esquerdo quanto do lado direito.
- Em limites finitos
Uma função tem um limite infinito se se aproxima do infinito positivo ou negativo à medida que a entrada se aproxima de um valor específico. Isso é denotado como
limão x → c f (x) = ± ∞.
- Limites no infinito
Este tipo de limite descreve o comportamento de uma função conforme a entrada se aproxima do infinito positivo ou negativo.
limão x → ± ∞ f(x) = eu
Propriedades do Limite
Existem diversas regras e propriedades de limites que podem ser usadas para simplificar e avaliar limites.
Deixei lim x → c f(x) e lim x → c g(x) existir e k é qualquer constante. Então
A regra constante
O limite de uma função constante é a própria constante.
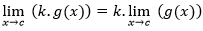
A regra da soma e diferença
O limite da adição ou subtração de duas funções equivale à adição ou subtração dos seus limites.
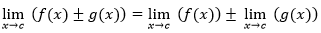
A regra do produto
O limite do produto de duas funções é o produto dos seus limites.

A regra do quociente
O limite do quociente de duas funções é o quociente dos seus limites. No entanto, o limite fornecido do denominador não é zero.
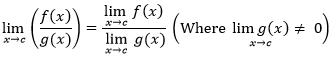
Regra do Poder
O limite de uma função potência é a potência do limite da função base.
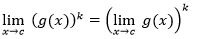
Técnicas para encontrar o limite
Aqui estão alguns métodos comuns para encontrar limites:
Substituição Direta: A técnica básica é inserir o valor limite na função. Se a função for válida nesse valor, o limite é igual ao valor da função naquele ponto específico.
Factoring: Em alguns casos; a função pode ser simplificada por fatoração. Isso pode eliminar fatores comuns no numerador e no denominador, facilitando a determinação do limite.
Regra de L Hopital: Esta regra é usada quando o limite resulta em uma forma indeterminada (0/0 ou ∞/∞) . A Regra de L Hopital permite a diferenciação do numerador e do denominador para simplificar o limite.
Usando uma calculadora de limite : Para funções complexas ou ao procurar uma verificação rápida, ferramentas como a calculadora de limite da AllMath podem calcular o limite instantaneamente. Esta abordagem digital pode ajudar na verificação dupla de cálculos manuais e pode ser especialmente útil ao lidar com expressões difíceis .
Limites Comuns: Memorize os limites comuns que surgem com frequência.
- limãox → 0 (1 – cos x) / x = 1
- limãox → 0 (Sen x / x) = 1
- limãox → 0 (tan x / x) = 1
- limãox → 0 (1 + x ) (1/x) = e
- limite x → ∞ (ex ) =∞
- lim x → – ∞ (ex ) = 0
Exemplos resolvidos de limite
Vejamos alguns exemplos resolvidos para esclarecer o conceito de limite.
Exemplo 1:
Encontre o limite quando x se aproxima de 3 para a função f(x) = 2x 2 – 5x + 6.
Solução:
limãox → 3 (2x 2 – 5x + 6)
=limx → 3 (2x 2 ) -limx → 3 (5x)+limx → 3 (6)
= 2 limx → 3 (x 2 ) – 5 limx → 3 (x)+ 6 limx → 3 (1)
Aplicar o limite
=2 (3 2 ) – 5 (3)+ 6 (1)
=18 – 15 + 6
=9
Assim, limx → 3 (2x 2 – 5x + 6) = 9
Exemplo 2:
Calcular limitex → 1 [(x 2 – 1) / (x – 1)].
Solução:
limãox → 1 [(x 2 – 1) / (x – 1)] = 0/0 (Esta é uma forma indeterminada)
∴ (x 2 – 1) = (x – 1) (x + 1)
limãox → 1 [(x 2 – 1) / (x – 1)] ⇒ limitex → 1 [(x – 1)(x + 1) / (x – 1)]
Como (x – 1) será cancelado
limãox → 1 [(x 2 – 1) / (x – 1)] = limitex → 1 (x + 1)
= 1 + 1 = 2
∴lim _x → 1 [(x 2 – 1) / (x – 1)] = 2
Exemplo 3:
Avaliar limitex → 0 [(e x – 1)/(x)]
Solução:
limãox → 0 [(e x – 1)/(x)] (forneça forma indeterminada após aplicar limite direto)
Aplique a regra de L Hopital tomando as derivadas do numerador e do denominador em relação a x:
[( d( e x – 1)/dx) / (d(x)/dx)] = (e x – 0) / 1
limãox → 0 [(e x – 1)/(x)] = limitex → 0 e x = e 0
= 1
Portanto, o limite de (e x – 1)/x quando x se aproxima de 0 é 1.
Confira também sobre: a importância da segurança cibernética.
Resumo
Exploramos o conceito fundamental de limites em cálculo e discutimos vários tipos de limites e técnicas para sua avaliação. Também fornecemos exemplos para ilustrar como calcular limites em diferentes cenários.
Compreender os limites é crucial para vários aspectos da análise matemática, incluindo continuidade, diferenciabilidade e integração. Ao compreender os conceitos e técnicas apresentados aqui, você poderá navegar no mundo do cálculo e da análise matemática com confiança.
